Pesquisas eleitorais e a Margem de Erro (Tutorial)

Introdução

Nesse primeiro tutorial do site PollingData, vamos tentar explicar o que é Margem de Erro de forma intuitiva, porém também vamos apresentar algumas formulas básicas que são importantes para um entendimento completo do assunto.

Como esse é o primeiro tutorial, ainda não tenho certeza sobre qual deve ser o formato dos tutoriais. Gostaria que esse tutorial fosse útil tanto para estatísticos quanto para pessoas que tenham interesse em pesquisas eleitorais porém não têm o conhecimento técnico do assunto. Ou seja, acho importante incluir algumas fórmulas para definir de forma precisa alguns conceitos, porém quero que o texto seja compreensível sem elas.

A grande maioria do material apresentado abaixo faz parte de minha tese de Doutorado, com alguns ajustes para facilitar a compreensão por não-estatísticos.

Algumas definições

Como um exemplo introdutório, vamos pensar nas pesquisas de intenção de voto que são constantemente divulgadas na mídia. Os institutos de pesquisa selecionam uma amostra da população com o objetivo de estimar a intenção de voto da população em cada candidato. Ou seja, o objetivo é entrevistar apenas algumas centenas de pessoas sobre qual candidato pretendem votar, e apartir dessa informação, estimar a intenção de voto de toda a população. Utilizar algumas centenas de entrevistas para prever a atitude de milhares de pessoas. Além de ser impossível entrevistar todas as pessoas, utilizar uma amostra tem claras vantagems em relação à custo/tempo. E em muitos casos, de qualidade também. Porém os resultados são menos precisos, como veremos a seguir.

Para estimar a intenção de voto, utiliza-se um estimador, que é qualquer função que dependa somente da amostra (dos dados), ou seja, não pode depender de quantidades desconhecidas, como por exemplo da inteção de voto de pessoas que não estejam na amostra. O estimador é o que permite “transformar” os resultados da pesquisa em resultados da população toda. Apesar dos resultados apresentados nessa seção serem válidos para diferentes estimadores, estamos mais interessados no contexto de proporções populacionais, pois esse é o cenário usualmente considerado em pesquisas eleitorais. Nessa seção iremos denotar o estimador da proporção de votos do candidato i por \(\hat{P_i}\) e a proporção real de votos na população (parâmetro populacional) por \(P_i\).

A definição de um estimador é vaga. É possível utilizar diversas funções diferentes para obter estimadores. Existe uma infinidade de possíveis estimadores. Porém quando fazemos uma pesquisa, iremos divulgar apenas um resultado, então temos que escolher apenas um estimador. Como determinamos qual é o melhor estimador? Essa é a pergunta mais importante pra se fazer! A resposta é: comparando a performance dos diferentes estimadores.

A forma com que os estimadores são calculados é motivo de grande discussão e polêmica na estatística. Brigas também. O que você tem que saber é que não existe uma única forma de comparar os estimadores. Não existe um estimador que seja melhor que todos os outros em todos os cenários e/ou situações possíveis. Por isso a grande dificuldade. Por isso que para se fazer pesquisa, é necessário tanto conhecimento teórico quanto prático, juntamente com bastante bom senso.

No contexto de amostragem, de pesquisas eleitorais, a forma mais usual (tradicional) de se comparar a performance dos estimadores é através da distribuição amostral. A distribuição amostral de um estimador descreve o comportamento do estimador em todas as possíveis amostras selecionadas. Conceitualmente, imaginana-se infinitas replicações do desenho amostral e calcula-se o valor do um estimador em cada particular amostra. Ou seja, dessa forma podemos comparar a performance dos diferentes estimadores analisando o comportamento geral dos estimadores. Por exemplo, na média de todas as possíveis amostras, qual estimador está mais próximo do valor real da população. Claramente esse é um exercício teórico, pois se soubéssemos qual é a intenção de voto da população no candidato i, não haveria a necessidade de fazer pesquisas.

Performance dos estimadores

Nesse contexto, a qualidade do par estimador/amostragem é avaliada por meio de dois critérios básicos resultantes de sua distribuição amostral:

• Vício do Estimador É uma medida de quanto, ao longo das infinitas replicações, é a diferença média entre o estimador e a quantidade populacional sendo estudada.
• Variância do Estimador É uma medida de quanto, ao longo das infinitas replicações, os valores do estimador nas diferentes amostras variam, ou o oscilam, em torno de sua média.

O ideal é que o estimador tenha um vício pequeno, ou seja, que em média ele acerte o valor do parâmetro populacional, e que tenha uma variância pequena, ou seja, que os diferentes valores que o estimador assumiria em cada possível amostra não sejam muito diferentes uns dos outros. A maneira mais intuitiva de entender esses conceitos é fazendo uma analogia com um alvo, onde cada uma das quatro figuras no gráfico 1 abaixo representam os arremessos de dardos de quatro jogadores diferentes, denominados (a), (b), (c) e (d). O objetivo é acertar o ponto vermelho no alvo. O jogador (a), em média, erra o ponto vermelho, ou seja, ele têm um arremesso viciado no sentido de consistentemente arremessar o dardo mais para para o lado direito do alvo, e além disso, o resultado de cada arremesso varia bastante, ou seja, sua mira não é muito precisa. O jogador (a) é o pior dos 4 jogadores. Já o jogador (b), apesar de a sua mira não ser muito precisa, pois o resultado de seus arremessos variam bastante, em média acerta o alvo. O jogador (c) tem a mira bastante precisa, pois os resultados de seus arremessos sempre ficam muito próximos uns dos outros, porém em média ele erra seus arremessos. É difícil dizer entre os jogadores (b) e (c) qual é o melhor, porém eles são claramente melhores do que o jogador (a). O melhor jogador de todos é (d), pois ele é preciso e em média acerta o alvo.

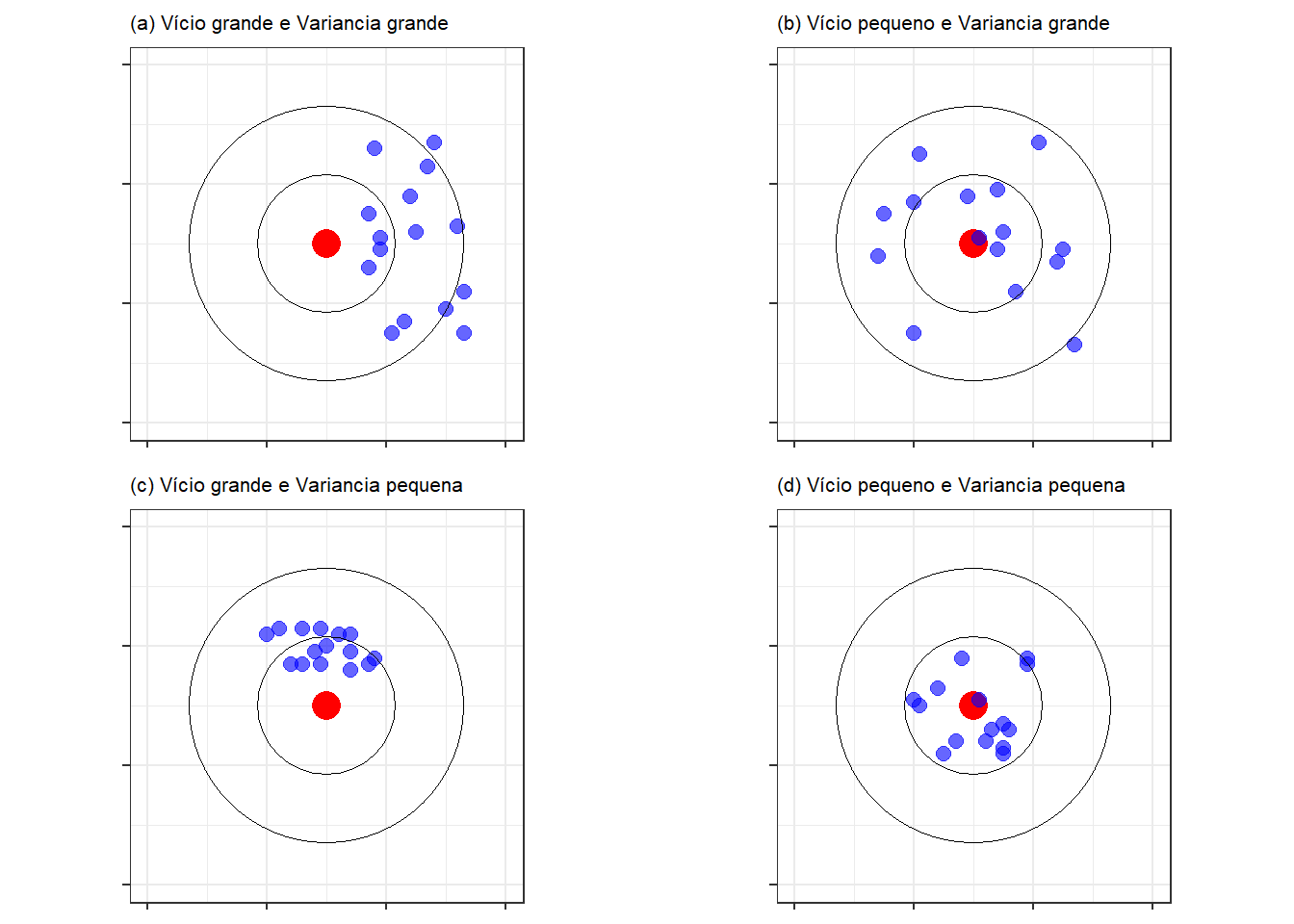
Figure 1: Figura 1: Importância do Vício e da Variância

O alvo em questão é a quantidade populacional de interesse, ou seja, no contexto de pesquisas eleitorais é a intenção de voto em um determinado candidato. Como foi visto no exemplo, tanto o vício quanto a variância são importantes para avaliar um desenho amostral, ou seja, aqueles que em média têm uma performance melhor.

É importante notar que a qualidade de um estimador não está relacionada com a estimativa obtida para uma amostra específica, mas somente com a média dos valores que poderiam ser obtidos em todas as possíveis amostras. É uma lógica pré-experimental que perdura após a experimentação, não importando qual particular estimativa foi efetivamente observada. Quando calculamos o valor do estimador para uma particular amostra, esse valor obtido passa a ser denominado de estimativa.

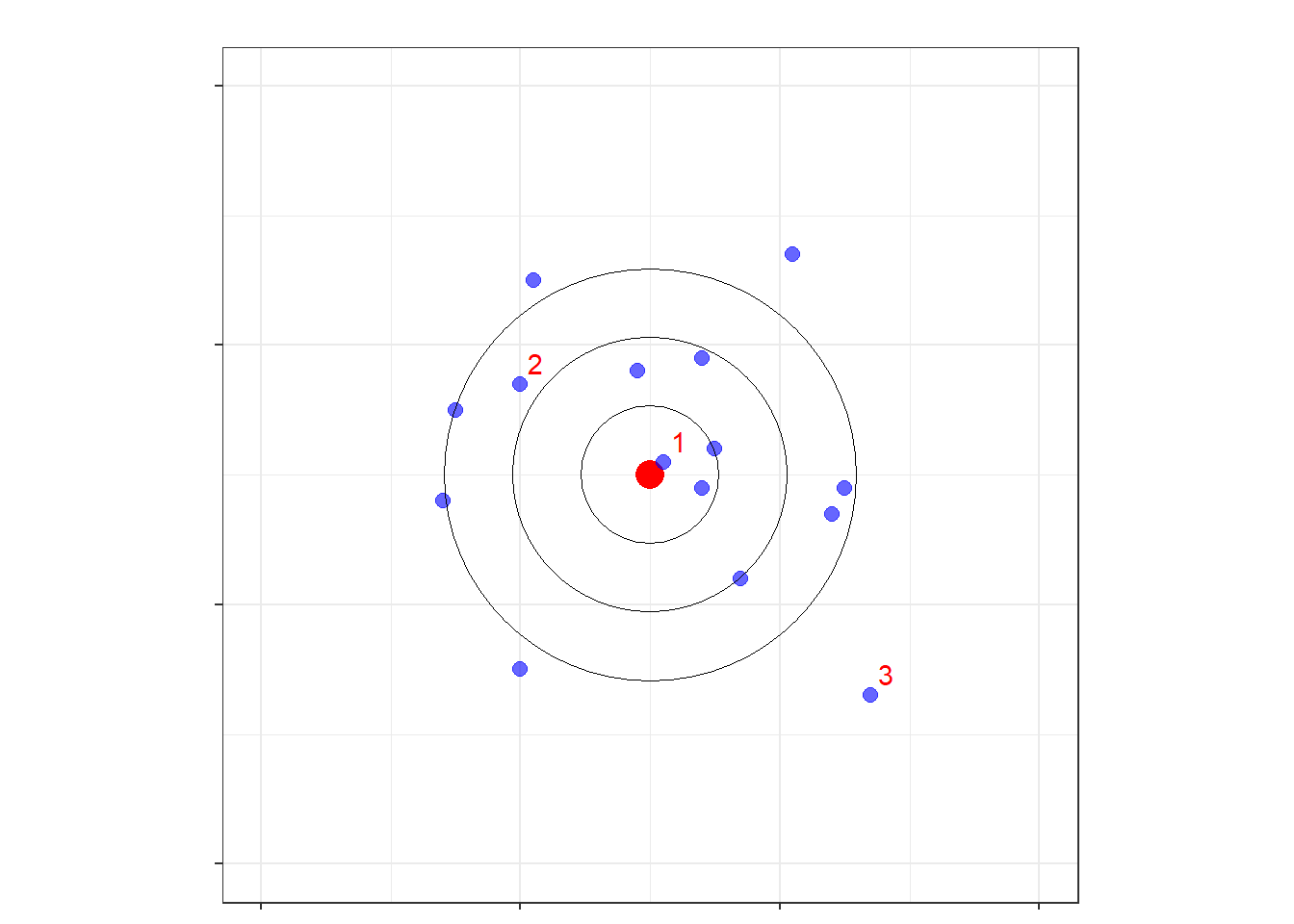
(#fig:alvo_b)Figura 2: Alvo do jogador (b)

Para explicar melhor esse ponto, na figura 2 desenhamos somente o alvo do jogador (b), e destacamos \(3\) resultados de arremessos feitos por ele. O arremesso \(1\) foi o melhor deles, bem próximo ao alvo vermelho em cheio, o arremesso \(2\) foi mediano e o arremesso \(3\) foi o pior de todos os arremessos feito pelo jogador. Apesar de o jogador (b) na média de todos os arremessos acertar ao alvo, isso não garante que um arremesso específico irá acertar o mesmo, mais que isso, é possível que nenhum dos arremessos acertasse o alvo. Além disso, apesar do mesmo jogador ter feito todos os arremessos, claramente alguns arremessos são melhores do que os outros, ou seja, têm um erro observado menor.

Analogamente, no caso do desenho amostral, por mais que o estimador utilizado seja não-viciado, isso não quer dizer que uma amostra específica tenha “acertado o alvo”. Além disso, algumas amostras serão melhores que outras, ou seja, terão um erro observado menor, mesmo tendo sido (hipoteticamente) geradas pelo mesmo desenho amostral. O erro observado para uma particular amostra pode ser definido como a distância entre a estimativa nessa particular amostra e a quantidade populacional que o estimador se propõe a estimar.

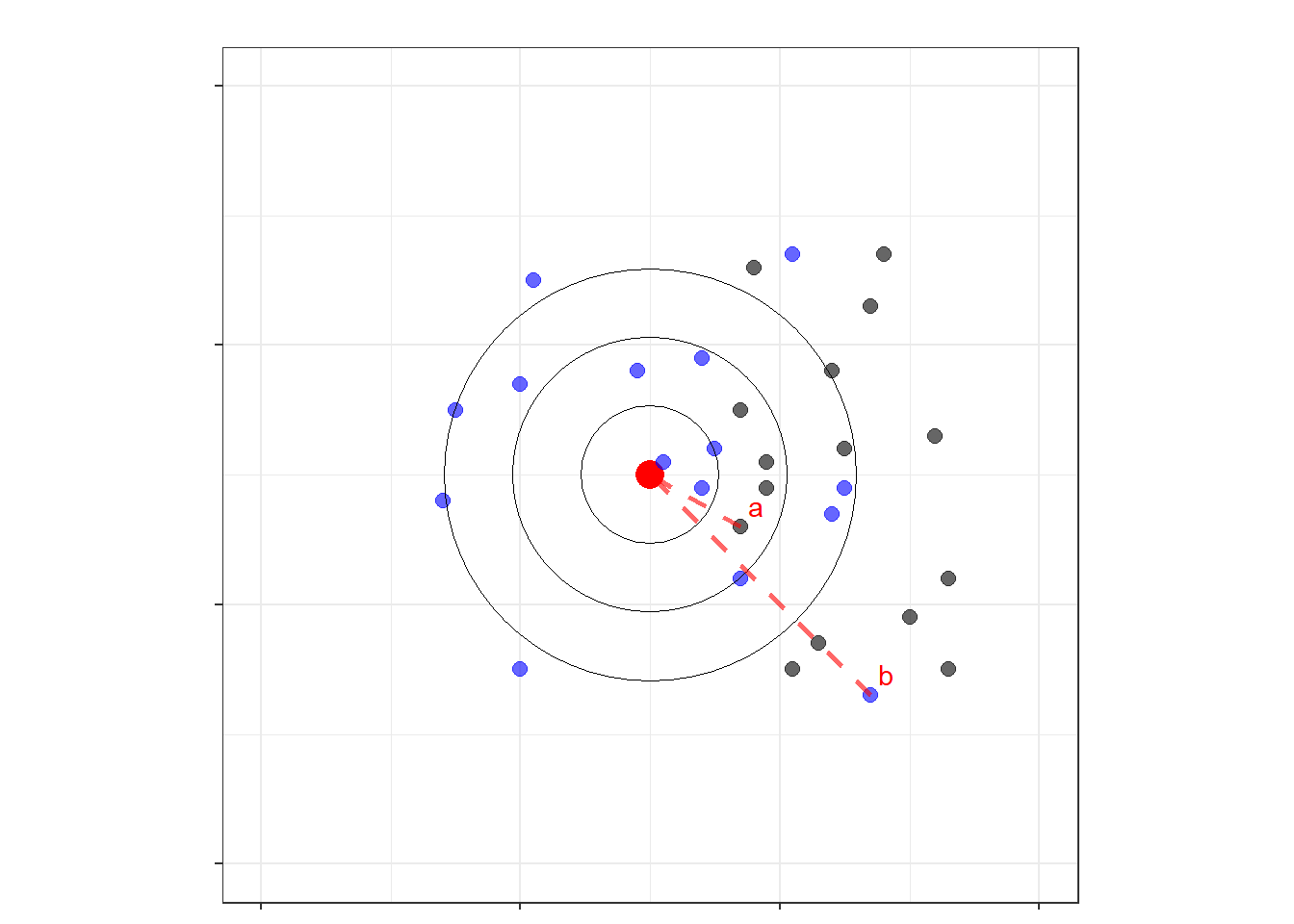
(#fig:alvo_ab)Figura 3: Alvos dos jogadores (a) e (b) sobre-postos

Seguindo a mesma linha de raciocínio, na figura 3 mostramos a sobreposição dos arremessos do jogador (b) em azul, e do jogador (a) em preto. Apesar do jogador (a) ser considerado o pior jogador pelo critério do vício, pois em média seus arremessos erram mais o alvo do que os outros jogadores, existem arremessos do jogador (a) que são melhores do que arremessos do jogador (b), como destacado na figura pelas linhas vermelhas achuradas.

O mesmo pode ocorrer com os diferentes pares de desenhos amostrais e estimadores, um estimador mais eficiente pode ter uma estimativa em uma amostra específica pior do que uma estimativa obtida de um estimador menos eficiente. Independentemente dessas possibilidades, até porque é impossível saber se algo do tipo ocorreu pois a quantidade populacional é desconhecida, estimadores são comparados segundo suas propriedades pré-experimentais, não importando o valor que o estimador tenha assumido em uma particular amostra.

Erro Amostral e a margem de erro

O erro amostral é a diferença entre a estimativa e a quantidade populacional a qual o estimador se propõe a estimar. Antes de selecionar a amostra, essa diferença pode ser representada por \(\hat{P_i} - P_i\) para o estimador \(\hat{P_i}\) da intenção de voto da população no candidato i representada por \(P_i\). Usualmente, é impossível avaliar essa diferença pois não conhecemos \(P_i\). Ou seja, quando observamos uma amostra e obtemos uma estimativa, não sabemos qual o erro amostral sendo cometido.

Um dos motivos que pesquisas eleitorais são envoltas em muita controvêrsia é justamente porque elas são um dos poucos casos onde é possível conhecer a intenção de voto real da população (\(P_i\)). Ou seja, em tese é possível saber qual foi o erro amostral observado pela pesquisa eleitoral. É importante ressaltar que mesmo conhecendo essa quantidade após a eleição, a intenção de voto é de fato um processo dinâmico, que muda com o tempo, então para calcular qual foi o erro amostral de uma pesquisa, o tempo tem que ser levado em consideração, além de outros fatores conhecidamente importantes, como percentual de indecisos na pesquisa.

Note que erro amostral se refere somente ao erro cometido por estimar uma quantidade populacional utilizando uma amostra. Existem outros tipos de erros não-amostrais que podem fazer com que mesmo um estimador não-viciado não coincida em média com a quantidade populacional de interesse. No exemplo dos alvos, seria o mesmo que um jogador que erra o alvo por causa de uma rajada de vento, por exemplo, e não por causa de sua mira.

Gostariamos de afirmar que “O valor absoluto do erro amostral dessa pesquisa é menor ou igual a \(d\)%”, onde \(d\) é uma constante arbitrariamente pequena. Em pesquisas eleitorais, usualmente chama-se \(d\) de margem de erro. Apesar de não ser possível avaliar a estimativa \((\hat{P_i} - P_i)\) para a amostra que foi efetivamente selecionada, é possível conhecer o seu comportamento ao longo de todas as possíveis amostras (utilizando a suposição de amostragem probabílistica).

Ou seja, podemos quantificar \((\hat{P_i} - P_i)\) de uma forma um pouco diferente. Podemos afirmar, por exemplo, que “Antes da amostra ser selecionada, o valor absoluto do erro amostral da pesquisa tinha uma probabilidade de \((1-\alpha)\)% de ser menor do que d%”. Apesar da segunda afirmação ter uma probabilidade associada, ela também tem muita força. Para formalizá-la matematicamente, três quantidades devem ser definidas:

• Confiança \((1-\alpha)\) - a confiança que gostaríamos de ter, ou seja, especificar qual probabilidade queremos associar a \(d\).

• Erro amostral \((d)\) - o erro amostral desejado, ou seja, qual \(d\) é considerado suficiente.

• Tamanho amostral \((n)\) - o tamanho da amostra, ou seja, quantas entrevistas serão realizadas.

Matematicamente, a frase acima pode ser enunciada como:

\[P(|\hat{P_i} - P_i| \leq d) = 1 - \alpha\].

É muito comum divulgar os resultados de uma pesquisa como sendo \(\hat{P_i} \pm d\). Essa forma de apresentar os resultados de uma pesquisa é denominada de Intervalo de confiança da quantidade de interesse. Essa forma é bastante usada pois mostra os resultados de uma pesquisa levando em conta a margem de erro, ou seja, a precisão da estimativa. A interpretação do intervalo de confiança usualmente causa bastante confusão. Teoricamente, o intervalo quer dizer que, se em toda possível amostra selecionada esse intervalo for calculado com a estimativa obtida \(\hat{P_i}\), esses intervalos irão conter a quantidade populacional real \(P_i\) em \((1 - \alpha) \%\) das amostras. Novamente, essa probabilidade associada ao intervalo é pré-experimental, ou seja, antes da seleção da amostra, porém depois de observada a amostra, o intervalo de confiança calculado para essa amostra específica ou contém ou não contém o parâmetro populacional.

Por exemplo, imagine que uma fábrica produz canetas, das quais \(1,3 %\) são defeituosas, não escrevem. Imagine que o João foi numa loja comprar uma única caneta dessa marca. No ato da compra, ele tem uma probabilidade de \(0,987\) de comprar uma caneta que funciona. Depois que ele comprou a caneta, levou-a pra casa e tentou escrever com ela, não existe mais probabilidade associada a caneta. Ou ela funciona, ou ela não funciona. Ou seja, depois de realizado o experimento, no caso a compra de uma particular caneta, não importa mais qual era a probabilidade da caneta ser defeituosa, pois aquela caneta é ou não defeituosa. A dificuldade com amostragem é que como o parâmetro populacional \(P_i\) é desconhecido na maioria dos casos, nunca sabemos se o intervalo de confiança daquela particular amostra contém ou não o parâmetro populacional.

Voltando aos exemplos dos alvos, imagine que os jogadores não estão mais arremessando dardos, que seriam os equivalentes as estimativas pontuais \(\hat{P_i}\), agora eles estão arremessando argolas, que seriam o equivalente as estimativas intervalares \(\hat{P_i} \pm d\), e o alvo pode ser interpretado como um pino. Se uma particular argola é arremessada e contém o pino no seu interior, seria o equivalente do intervalo de confiança conter o parâmetro populacional. Ou seja, apesar de existir uma determindada probabilidade à priori das argolas acertarem o alvo para cada jogador, cada arremesso contém ou não contém o pino.

Além disso, podemos imaginar o raio da argola como sendo determinado pela confiança \((1-\alpha)\). Se uma argola tiver um raio maior, a sua confiança é maior do que era com a argola menor, pois quando o jogador estiver arremessando a argola maior, ele terá uma probabilidade maior de acertar o alvo, como podemos ver na figura 4, onde as argolas são representadas por círculos vermelhos em torno do arremesso. Claramente é mais difícil de acertar o alvo usando as argolas em (a) do que utilizando as argolas em (b). O mesmo ocorre com o intervalo de confiança, aumentar a confiança do intervalo aumenta a largura do intervalo, e será mais fácil de um intervalo conter a quantidade populacional.

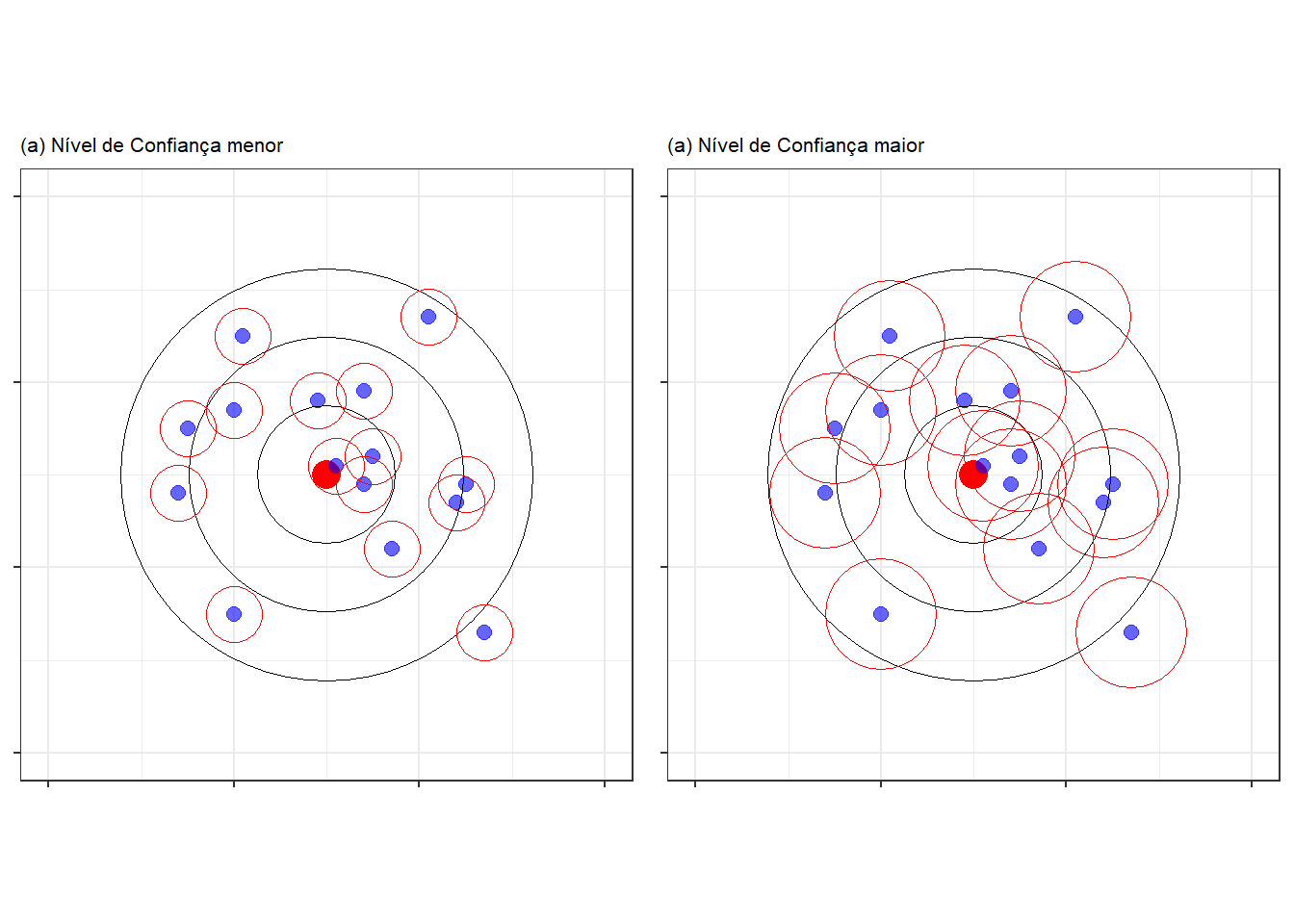
(#fig:alvo_ic)Figura 4: Precisão dos Intervalos de Confiança

Alterar a confiança do intervalo de confiança não tem nenhum ganho real, pois apesar de aumentar a probabilidade de acerto, na verdade a precisão do intervalo diminue, pois um erro observado maior deixa de ser considerado um erro. Ou seja, uma pessoa que passa a arremesar uma argola maior, vai acertar mais o alvo, mas isso não quer dizer que a sua mira melhorou, o que aumentou foi o raio da argola, e uma distância que na argola menor era considerada como um erro, agora passará a ser considerada como um acerto.

A única forma de realmente melhorar a eficiência do intervalo de confiança é manter o mesmo nível de confiança porém diminuir a largura do intervalo. Isso só é possível se a variância do estimador diminuir, o que por sua vez só é possível aumentando o tamanho da amostra, uma vez que a variância do estimador \(\hat{P_i}\) depende de \(\frac{1}{n}\). Pensando no exemplo das argolas, manter a probabilidade de uma jogador acertar porém diminuir a largura da argola não parece ser fisicamente possível. Para faciliar a compreensão, imagine que aumentar o tamanho da amostra seria o equivalente do jogador dar um passo em direção ao alvo, aumentado assim a sua probabilidade de acertar o alvo, mesmo com um disco de mesmo raio.

Nesse exemplo dos alvos, o comprimento do raio pode ser interpretado como o erro amostral \(d\). Ou seja, deve estar claro que dizer a margem de erro de uma pesquisa sem especificar qual foi a confiança (% de acerto) não diz qual é a precisão da pesquisa. Usualmente, a confiança é fixada em \(95%\), mas mesmo a confiança deve ser explicitamente divulgada juntamente com os resultados de uma pesquisa.